I want to begin this post with its high-sounding title by bucking the trend regarding what the worldwide SEO community says and regarding what I generally claim. In a certain sense I am going against what I myself believe, but that is precisely the point: “What we believe in and our general convictions cannot be applied to SEO or to data analysis”.

The list of such things where the lack of credibility in one’s own beliefs should alarm us could be very long, but I don’t want to spend too much time on it … so let’s take user tests as an example.
Why do they tell us that the Author Snippet causes an increase in the CTR?
The answer is simple. They tell us that because one fine day, starting from the appearance of their face on a SERP, their traffic increased, however:
- I haven’t seen a detailed analysis in any post of how, where, when or why their traffic increased.
- I haven’t seen considerations in any post on the variables considered in order to reach the conclusion that the increase in the CTR is as a result of the Author Snippet.
- I haven’t seen how to extrapolate the data from the CTR with certainty in any post, or where this data highlights a decisive increase.
Why do these case histories make no difference?
The answer is simple. In SEO and in general when you deal with people it depends. But what does it depend on? It depends on many factors and many subtle and petty variables which we tend to ignore due to laziness or simple lack of attention. Here is a list of some such cases where our data analysis may not be accurate:
- There are queries where the CTR could be influenced by the Google News box.
- We need to analyse the queries where our position is constant.
- We need to consider which browser the searches come from.
- We need to consider which device is used to carry out the search.
- We need to evaluate the impact of “Not Provided” keywords.
- We need to evaluate if the search is carried out by someone logged in to Google or not.
- We need to evaluate if the search is carried out by someone in your circles.
- We need to evaluate if your post has been +1’d from people in the circle of the user who carried out the search.
- We need to consider the possibility that the user doesn’t click on the result but goes to the author’s G+ profile.
- We need to remember the existence of AdWords.
- We need to consider that some content mixes Authorship and Video Snippet.
- There are other possible scenarios … due to the incredible personalisation of search results.
Given the above it becomes rather obvious that knowing with certainty how much the impact of the snippet on the CTR is positive or negative becomes extremely difficult. The only solution is to get a more complete data instrument from Google within the webmaster tools which indicates the CTR of the number of searches with scientific evidence for a specific query, both with the appearance of the author snippet and without.
Let’s take a few hypothetical scenarios.
Scenario 1
I’m browsing using my Galaxy Note and if I type the same search on Chrome and Firefox I get different results:
- Chrome shows me the author snippet
- Firefox doesn’t show the author snippet
How can you evaluate what has influenced the CTR in the data analysis phase if you don’t know how many times a similar scenario has happened?
Scenario 2
Dan Petrovic is in my circle.
Dan Petrovic has +1’d Richard Greenwood’s Live SEO Audit post.
I run a search while logged in to Google.com for the keywords “Live SEO Audit dejan seo” and find the snippet with the +1 social annotations [1]. [NB: the example is intended to show what I mean by the +1 social annotation]
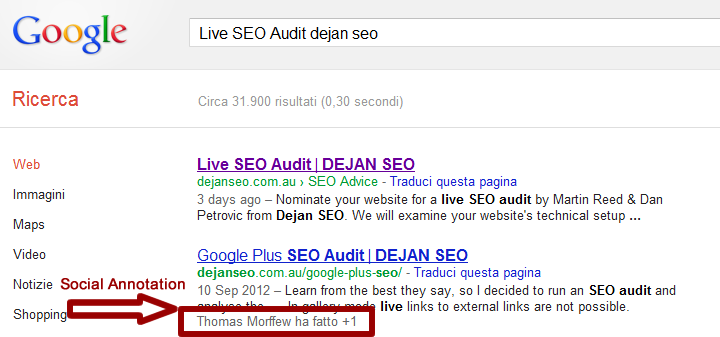
In this case the user in my circle is Thomas but it’s the same.
In most cases the social annotations have the upper hand over author snippets. In this case your statistics will show “Not Provided”.
How can you evaluate what influenced the CTR in the data analysis phase if you don’t know how many times such a scenario has happened?
Why do they talk about the CTR so often instead of the real value of the Author Rank and the use of Authorship as a well-defined marketing strategy?
Most SEO articles and most SEO consultants I have heard speak about Authorship as a certain CTR multiplier, especially after the claims made by John Mueller and Sagar Kamdar [2] – who maintain that there is no Author/Agent Rank [3].
The problem is that the question is not being dealt with from the correct point of view. We tend to want to impose the perception that we have regarding the importance of authorship applied to our sector, or rather, to our situation. We have an excessive opinion of Google and as SEO writers we know that being reliable is important in our sector. The tendency to create a consultant profile of a certain level makes us think it is extremely important to enjoy a high level of visibility, prestige and credibility.
We know why it is very clear to us at a strategic level, that the prestige as professionals in our sector is a key point for the near future, but this strategy cannot be considered valid or applicable always or absolutely, or rather may not mirror the strategic choices of a customer or a specific niche.
Apart from this the blindness with which they say that the impact on the CTR becomes apparent is certainly positive and disconcerting. I ask you to think about this point carefully and to check your data with a little less narcissism.
I can guarantee that on busy sites with huge volumes of searches (and where no competitor has implemented author mark-up) the impact of the author snippet has not only not produced significant benefits, but has even brought about a decrease in the number of clicks when seen at a glance (just like all those seen online until now).
This is only a stupid example where 3bmeteo has adopted an editorial strategy created by real people in a completely virgin sector regarding authorship, but without having any positive feedback in terms of numbers, or rather, in terms of analysable numbers – because that is what we’re talking about.
It is precisely for this reason that I want to underline that reading is not enough, it is important to analyse and find out for yourself while remaining critical and keeping all the variables of the game in mind.
Aiming for people is a strategic choice.
I am aware that it is much simpler to convince people by offering short term numbers and trivial reasons, but based on my personal experience I can say that we need to be able to give up our own beliefs and try to understand the best way to go for the good of the project you are working on.
It is not a matter of SEO, it is not a matter of CTR.
Implementing rel=author is and must be a conscious strategic choice, a strategic choice aimed at having confidence in and giving visibility to the people who are part of our team. If the web project is not geared towards the creation and valorisation of people, but only towards the strengthening of a brand (for example), there is no point in forcing your hand just for a few extra clicks (or perhaps for a few less clicks).
SEOs are still making the same errors of the past in a ciclic way…focusing on the wrong things.
Scenario: a few less clicks today, a loyal user tomorrow.

Precisely in reference to that provocative “a few less clicks” let’s hypothesise a possible scenario in this case too.
Let’s imagine that the user carries out a search and finds my result with my lovely face. My lovely face intrigues them and instead of clicking on the blue title they click on my name and surname and are therefore rerouted to my G+ profile.
How can we evaluate this situation? Positive or Negative?
In my opinion this depends on the profile and it depends on what the user does next. If they add me to their circle then I’ve hit the jackpot and that one click less is priceless, while if they don’t add me I’ll have lost a click.
This begs two questions:
- In this case what is the value of a lower CTR?
- Should a strategy be based on CTR value?
I would like to begin a discussion on these points together with you.
The Author Rank is a question of trust.

Even if we are not certain that it is actually a small piece of the puzzle in Google and Bing searches, the prestige of the people who make up our team are not only a strategic vision for the purposes of marketing, but also a real relationship of trust which we put back into them.
This trust is the same trust that search engines put back into us as people and as websites.
We don’t make the mistake of considering the Author Rank a search result manipulator because the intended objective is not and never will be this.
It is extremely difficult and takes guts to put your head into a crocodile’s mouth, but it is very simple to lose your head.
Think strategically, Not Numerically!
Riferimenti
[1] Social Annotation in web search
[2] Google Authorship: An Interview with Google’s Sagar Kamdar
Image Credits: Credits: http://bit.ly/OA4NFH
Dan Petrovic, the managing director of DEJAN, is Australia’s best-known name in the field of search engine optimisation. Dan is a web author, innovator and a highly regarded search industry event speaker.
ORCID iD: https://orcid.org/0000-0002-6886-3211

I bet if you had a picture of a pretty girl in the SERPs, that would include the click thru rate…I’m basically positive. Women could have the most authorship in 5 years and be the “go to” content creators…just sayin.
Hi Jason we already try with a Pretty Girl, but without any positive result!
It’s not a mattero of boys or girls.
I didn’t know there was a myth about the impact of authorship on CTR. Most people still haven’t figured out how to implement it properly.
It’s one of those logical things, even those who don’t have it implemented think that those who did, get the advantage as people click more on “authored” results.
That’s interesting, but it would greatly depend on the type of search. (e.g. “I’m bored” vs “human rights in china”)
I guess, but I’d never approached it from that angle. I look at it from the larger perspective of “structured data” and the benefits that that brings.
I think the CTR angle is a bit of red herring, and if people are selling it on that basis then that’s very misguided. As the article points out, authorship needs to be a strategic approach.
I have a travel blog where the writer is actually a pretty blond girl with a nice figure. I asked if I could use a headshot of her and she agreed. It was perfect, blond, smile, bright red dress showing ample assets. Couldn’t have faked it better. Implemented rel=author and got the image showing almost immediately Guess what. ZERO CTR impact. Oh well, back to the drawing board.
The way to test this is by implementing the authorship on an article, then changing the image around testing if different images have different CTR. If there is no difference in results then your point is valid. However if there is a difference in CTR and the only thing that is changing is the image then there is your evidence.
Cyrus Shepard wrote an article about these tests on SEOmoz. seomoz.org/blog/google-author-photos
The Cyrus Shepard post show a very ugly starting image. It’s a little bit different, but the point is not there in my opinion.
But if the image has no impact on CTR then it doesn’t matter how ugly the photo is.
Yes and that is the point.
The SEO field is full and crowded of Rich and Authored Snippet so probably a better face can make you stand out, but in all the analysis I saw there are too many factors not taken into account and I explained here way.
That is the point and in a clean serp like mine the results are clear…so the CTR is only a simple way to convince people to use it, but it’s the wrong way to do.
I have one site I am testing the author code on, my image shows up in search below the listing. I haven’t seen an increase. I love the concept of your article because we sure should have some real data behind all the bla bla bla. I actually think the authorship code is a way for google to track your influence so they can guide it how they may. OOps he runs too many sites and has too much influence bam seccond page.
All sorts of ways to eliminate the warning message “Automatically detected on the webpage author name: Not Found” always fails 🙁 .